Given that :
The avearge(mean) time patrons spend on the treadmill is
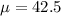
The standard deviation is

We now need to calculate the Z- score for 30 minutes and 40 minutes

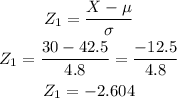
Similarly,
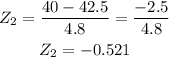
Therefore,
[tex]\begin{gathered} Pr(Z_1
Therefore, the probability that a randomly selected individual would spend between 30 minutes and 40 minutes on the treadmill is 0.2965 (to four decimal places)