In order to solve this, we have to use the compound interest formula given by the following expression:

Where r is the interest rate, P is the initial amount deposited, n the number of times the period is compounded a year, t the year, and A the final amount.
By replacing 0.0645 (6.45%) for r, 4 for n, 3 for t and 5500 for P into the above equation, we get:
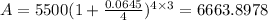
Then, after 3 years you will have $6663.9.
In order to determine the APY, we can use the following formula:
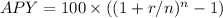
Where n is the number of times the interest is compounded a year (4) and r is the rate of interest (0.0645), then we get:
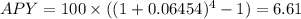
Then, the APY equals 6.61%