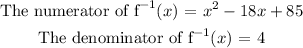Question

Find the inverse of the function below. When typing your answer use the "^" key (shift+6) to indicate an exponent. For example, if we have x squared (x times x) we would type x^2.()=9+4−4‾‾‾‾‾‾√f(x)=9+4x−4The numerator of −1()f−1(x) is Answer -Answer +Answer The denominator of −1()f−1(x) is Answer

Answer 1

Given:

There are given that the function to find the inverse is:

`f(x)=9+\sqrt[]{4x-4}`

Step-by-step explanation:

To find the inverse of the given function, first, we need to exchange f(x) into y, then exchange the variable which means change y to x and x to. Then, find the value of y.

Now,

Step 1:

Exchange f(x) into y:

`\begin{gathered} f(x)=9+\sqrt[]{4x-4} \\ y=9+\sqrt[]{4x-4} \end{gathered}`

Step 2:

Exchange the variables which means exchange y into x and x into y:

`\begin{gathered} y=9+\sqrt[]{4x-4} \\ x=9+\sqrt[]{4y-4} \end{gathered}`

Step 3:

Solve the above function for the value of y:

So,

`\begin{gathered} x=9+\sqrt[]{4y-4} \\ x=9+2\sqrt[]{(y-1)} \\ 2\sqrt[]{(y-1)}=x-9 \\ \sqrt[]{(y-1)}=(x-9)/(2) \end{gathered}`

Then,

`\begin{gathered} \sqrt[]{(y-1)}=(x-9)/(2) \\ (y-1)^{(1)/(2)}=(x-9)/(2) \\ y-1=((x-9)/(2))^2 \\ y=((x-9)/(2))^2+1 \end{gathered}`

Then,

`\begin{gathered} y=((x-9)/(2))^2+1 \\ y=(x^2-18x+81)/(4)^{}+1 \\ y=(x^2-18x+81+4)/(4) \\ f^(-1)(x)=(x^2-18x+85)/(4) \end{gathered}`

Final answer:

Hence, the numerator of the inverse function and the denominator of the inverse function are shown below:

`\begin{gathered} \text{The numerator of f}^(-1)(x)\text{ = }x^2-18x+85 \\ \text{The denominator of f}^(-1)(x)\text{ = 4} \end{gathered}`