Answer;
WUV = 36
Explanation:
Here is what we get when we draw the figures
Now we know that the sum of the interior angles of a triangle must equal 180 degrees; therefore,

Also, angle y and VWX are supplementary; therefore,
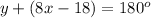
Now, solving for y in the above gives
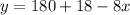
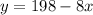
Putting this value of y in the first equation gives
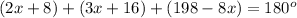
Expanding and simplifying the left-hand side gives
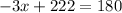
Subtracting 214 from both sides gives
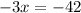
Finally, dividing both sides by -3 gives
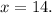
With the value of x in hand, we now find the measurement of WUV:

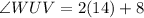

Hence, WUV = 36,