Question

(a)does the figure have reflectional symmetry? if so, give the n-fold number of the symmetry. (b)does the figure have rotational symmetry? if so, give the order and angle measure of the rotation.

Answer 1

(b) A figure is said to have an n-fold rotational symmetry if rotating through an angle of 360° / n does not change the figure.

In the case of the given figure, rotation through 180° does not change the figure.

Therefore,

`(360^o)/(n)=(180^o)/(1)`

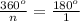
Cross-multiplying, we have

`\begin{gathered} 180^on=360^o \\ \text{ Dividing both sides by 180, we have} \\ n=(360^o)/(180^o)=2 \end{gathered}`

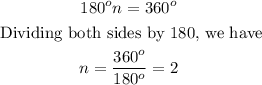
Hence, the order of rotation is 2 and the angle is 180°