Question

In 2011, the mean rate of violent crime (per 100,000 people) for 24 states west of Mississippi River was 406. The standard deviation was 177. Assume that the distribution of violent crime rates is approximately unimodal and symmetric. Between what two values would you expect tofind about 95% of the rates?a. 229 and 583b.52 and 760c. 229 and 406d.583 and 760

Answer 1

For this case we have the following parameters given for the rate of violent crime

`\mu=406,\sigma=177`

And we know that he distribution for the variable of interest is unimodal and symmetric so then we can assume that is approximately normal.

We can use the empirical rule who states that within two deviations from the mean we have 95% of the data from a normal distribution and we can calculate thge limits like this:

Lower limit

`406-(2\cdot177)=52`

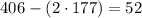
Upper limit

`406+(2\cdot177)=760`

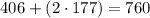
And then the solution for this case would be:

b. 52 and 760