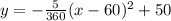Problem
A fireboat in the harbor is helping put out a fire in a warehouse on the pier. The distance from the barrel (end) of the water cannon to the roof of the warehouse is 120 feet and the water shoots up 50 feet above the barrel of the water cannon. Sketch a graph and find an exact equation of the parabola that models the path of the water from the fireboat to the fire. **Set up your drawing to where the parabola is in the middle of the x and y-axes.
Solution
For this case the width of the parabola needs to be 120 ft and then we can conlcude the center of the parabola at:
C= (120/2, 50)
C=(60,50)
Now we can calculate the equation with the following expression:
y= a(x-h)^2 +k
And for this case h=60, k= 50 and we have:
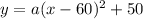
We also know that the point (0,0) is in the graph so we can use this point in order to find the value of a on this way:

And solving for a we got:

And we got:
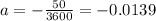
And then our equation would be: