Question

A 3.5-inch floppy disk in an old computer rotates with a period of 2.00 x 10^-1 s. Calculate the angular speed of the disk, the linear speed (in inches/sec) of a point on the rim of the disk, and the linear speed (in inches/sec) of a point 0.750 inches from the center of the disk. (Hint: a 3.5 inch floppy disk has a 3.50 inch diameter)

Answer 1

We have the next information

T=2.00 x 10^-1 s=0.2s

r=3.5 inch

For the angular speed

`\omega=(2\pi)/(T)`

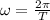
where omega is the angular speed, T is the period

We substitute

`\omega=(2\pi)/(0.2)=31.41\text{ rad/s}`

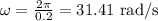
For the linear speed on the rim of the disc, we will use the next formula

`v=\omega\cdot r`

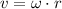
in this case r= 3.5/2=1.75 inch

`v=31.41(1.75)=54.97\text{ }\frac{inches}{\text{sec}}`

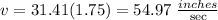
Then for the linear speed on the point at 0.750 inches from the center of the disk.

`v=31.41(0.750)=23.56\frac{inches}{\text{sec}}`

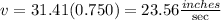
ANSWER

ω=31.41 rad/sec

v on the rim= 54.97 inches/sec

v on the point=23.56 inches/sec