We have two events:
A: sum of the numbers is less than 10.
B: sum of the numbers is a multiple of 3.
We can calculate the probabilities as a quotient of the "success" events and all the possible events.
The conditional probability P(B | A) is equal to the probability of P(A intersection B) divided by P(A). That is because, if A is given, then if B happens, A had also happen.
The "success" events for intersection A and B are:
{1,2}, {2,1}, {1,5}, {5,1}, {2,4}, {4,2}, {3,3}, {3,6}, {6,3}, {4,5}, {5,4}
There are a total of 11 results that belong to the intersection of A and B (sum less than 10 and multiples of 3).
Now, we calculate the results that correspond to event A:
{1,1}, {1,2}, {2,1}, {1,3}, {3,1}, {1,4}, {4,1}, {1,5}, {5,1}, {1,6}, {6,1}
{2,2}, {2,3}, {3,2}, {2,4}, {4,2}, {2,5}, {5,2}, {2,6}, {6,2}
{3,3}, {3,4}, {4,3}, {3,5}, {5,3}, {3,6}, {6,3}
{4,4}, {4,5}, {5,4}
There are 30 results that correspond to event A (sum is less than 10).
Then we can calculate P(B | A) as:
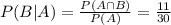
The conditional probability of B given A is P(B|A) = 11/30.