This is a question on present and
We are required to find out how much the future sums of the $2000 handed to them will amount to. This will test our knowledge on simple and compound interest.
Our approach is to take each one's case and analyse the appreciation or depreciation of the sums assigned using the appropriate formulae.
The compound interest formula goes thus:
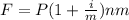
Where:
F = future sum
P = Present sum / Principal
i = interest rate
n = no. of years
m = number of compounding periods in a year.
The simple interest rate formula goes thus:

Albert:
Firstly, he had $1000 compounded monthly by 1.2%
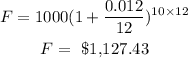
He lost 2% of $500 over the course of the 10 years.
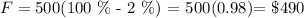
Firstly, he had $500 compounded monthly by 0.8%
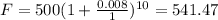
Total sum he gained over the course of the 10 years:
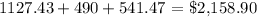
Marie:
Firstly, she had $1500 compounded quarterly by 1.4%
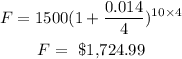
She lost $500 by 4% over the course of the 10 years.

Total sum gained by Marie over the course of the 10 years:
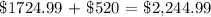
Hans
He had $2000 compounded annually by 0.9%
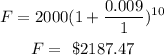
Total sum gained by Hans over the course of the 10 years:
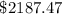
Max:
$1000 decreased in value exponentially at a rate of 0.5% annually.
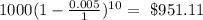
He had $1000 compounded biannually by 1.8%
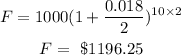
Total sum gained by Max over the course of the 10 years:
