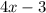Question

the rectangular garden has an area 8x^2+14x-15 square meters.if the length measures (2x+5)meters.find the width.

Answer 1

The area of a rectangle can be calculated with this formula:

`A=lw`

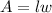
Where "l" is the length and "w" is the width of the rectangle.

In this case, you know that the area of the rectangle (in square meters) is represented with this expression:

`8x^2+14x-15`

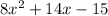
And the length (in meters) is represented with the expression:

`2x+5`

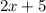
Then, you can substitute the expressions into the formula:

`\begin{gathered} A=lw \\ (8x^2+14x-15)=\mleft(2x+5\mright)w \end{gathered}`

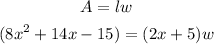
Now you need to solve for "w":

`\begin{gathered} (8x^2+14x-15)/(2x+5)=w \\ \\ w=(8x^2+14x-15)/(2x+5) \end{gathered}`

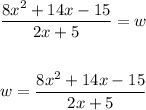
To simplify the expression, you can follow this procedure:

1. Factor the numerator as follows:

- Identify the coefficients:

`\begin{gathered} a=8 \\ b=14 \\ c=-15 \end{gathered}`

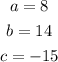
- Rewrite the middle term as a sum of two terms that makes that:

`\begin{gathered} a\cdot c=(8)(-15)=-120 \\ \end{gathered}`

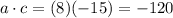
And whose sum is:

`b=14`

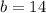
Then, this is:

`8x^2+14x-15=8x^2+(-6x+20x)-15=8x^2-6x+20x-15`

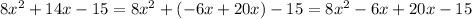
Because:

`\begin{gathered} -6+20=14 \\ \\ (-6)(20)=-120 \end{gathered}`

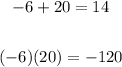
- Make two groups of two terms:

`=(8x^2-6x)+(20x-15)`

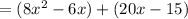
- Factor out the Greatest Common Factor from each group of terms. Notice that the Greatest Common Factor of the first group is:

`GCF=2x`

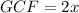
And the Greatest Common Factor of the second group is:

`GCF=5`

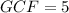
Then:

`=2x(4x-3)+5(4x-3)`

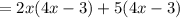
- Factoring out this Greatest Common Factor:

`(4x-3)`

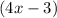
You get:

`=(4x-3)(2x+5)`

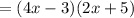
2. Substitute the factored numerator into the equation:

`w=((4x-3)(2x+5))/(2x+5)`

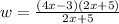
3. Since:

`((2x+5))/((2x+5))=1`

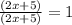
You get:

`\begin{gathered} w=(4x-3)(1) \\ w=4x-3 \end{gathered}`

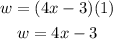
Therefore, you can determine that the answer is:

`4x-3`