Question

The volume of a rectangular prism whose dimensions are binomials with integer coefficients is modeled

by the function V(x)=x³-11x2 +31x -21. Given that x - 1 and x-7 are two of the dimensions, find
the missing dimension of the prism.
The missing dimension is___

Answer 1

Answer: x - 3

========================================================

Step-by-step explanation:

The -1 and -7 of x-1 and x-7 respectively multiply to (-1)*(-7) = 7

Let m be some unknown value such that 7m = -21. The solution is m = -3

This means (-1)*(-7)*(-3) = -21

Therefore the factorization is

`\text{x}^3-11\text{x}^2+31\text{x}-21 = (\text{x}-1)(\text{x}-7)(\text{x}-3)`

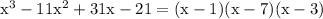
You can confirm this by expanding out the right hand side using the distributive rule. You should arrive at the original cubic after everything is simplified.

--------------

Another approach:

(x-1) and (x-7) are the two dimensions given to us.

They multiply to
`\text{x}^2-8\text{x}+7` using either the box method, distributive rule, or FOIL rule. Feel free to pick your favorite method.

Then the task from here is to compute
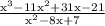`\frac{\text{x}^3-11\text{x}^2+31\text{x}-21}{\text{x}^2-8\text{x}+7}` using polynomial long division. Unfortunately synthetic division will not work because the denominator isn't linear.

The polynomial long division is shown below.