Question

The school that Rob goes to is selling tickets to the annual dance competition. On the first day of ticket sales the school sold 1 child ticket and 4 adult tickets for a total of $27. The school took in $36 on the second day but selling 4 child tickets and 4 adult tickets. What is the price of each of one adult ticket and one child ticket?

Answer 1

Step-by-step explanation

Let the price of one child ticket be x and the price of one adult ticket be y.

Therefore, from the given question, we will have;

`\begin{gathered} x+4y=27----i \\ 4x+4y=36-----ii \end{gathered}`

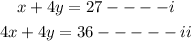
We can then create another equation iii from equation i

`x=27-4y----iii`

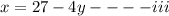
Substitute equation iii in equation i

`\begin{gathered} 4(27-4y)+4y=36 \\ 108-16y+4y=36 \\ 108-12y=36 \\ -12y=36-108 \\ -12y=-72 \\ y=(-72)/(-12) \\ y=6 \end{gathered}`

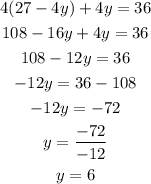
We can then substitute y=6 in equation iii

`\begin{gathered} x=27-4(6) \\ x=27-24 \\ x=3 \end{gathered}`

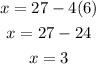
Answer: Cost of child ticket = $3 and Cost of adult ticket =$6