Question

Solve. 10 – |3x + 2| < 2 |18x + 12|

Answer 1

we have the inequality

10 – |3x + 2| < 2 |18x + 12|​

solve the inequality by using a graphing tool

so

see the attached image

please wait a minute

the solution is the shaded area

using a wolfrang Alpha

the solution in interval notation

(-16/39, ∞) and

(-∞, -12/13)

we have

the inequality

`10-\mleft|3x+2\mright|<2\mleft|18x+12\mright|`

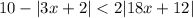
In this problem

`|18x+12|=6|3x+2|`

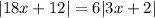
substitute

`\begin{gathered} 10-|3x+2|<2(6|3x+2|) \\ 10-|3x+2|<12|3x+2| \\ 10<13|3x+2| \\ \text{rewrite} \\ 13|3x+2|\text{ > 10} \end{gathered}`

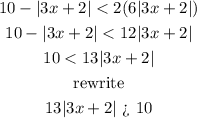
Find the First solution

`\begin{gathered} 13(3x+2)\text{> 10} \\ 39x+26>10 \\ 39x>-16 \\ x>-(16)/(39) \end{gathered}`

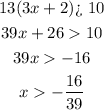
the first solution is the interval (-16/39, infinite)

Find the second solution

`\begin{gathered} 13\lbrack-(3x+2)\rbrack\text{> 10} \\ \text{Multiply by -1 both sides} \\ 13(3x+2)\text{ < -10} \\ 39x+26<\text{ -10} \\ 39x\text{ < -36} \\ x<-\text{ }(36)/(39) \\ \text{simplify} \\ x<\text{ }-\text{ }(12)/(13) \end{gathered}`

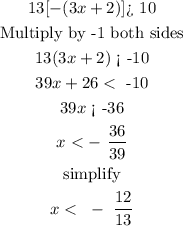
the second solution is the interval (-infinite, -12/13)