To solve this question we need to use the Euler's formula, to simplify the sine and cosine expressions:
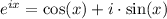
Using this formula, we can simplify the expression in the question to:
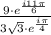
To calculate it easier, we can separate it in a product of two fractions:
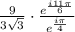
To simplify the first fraction we can rationalize it, multiplying the numerator and denominator by √3:
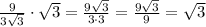
Now, to calculate the second fraction, we can use the property of dividing two exponencial numbers with the same base (we just need to subtract their exponents):
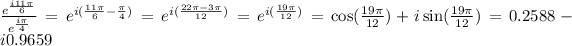
So the final expression is:
