Question

Hervenson is working two summer jobs, making $12 per hour at Mcdonald's and making $8 per hour washing cars. In a given week, he can work at most 20 totalhours and must eam a minimum of $200. If Hervenson works 15 hours at McDonalds, determine the minimum number of whole hours washing cars that he mustwork to meet his requirements. Write a system of inequalities to describe Hervenson's situation.

Answer 1

Data:

McDonalds: m

Washing cars: w

$12 per hour in m

$8 ér hour in w

m and w are the corresponding number of hours in each work

he can work at most 20 hours in total:

`m+w\le20`

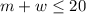
must earn a minimum of $200:

`12m+8w\ge200`

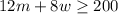
If he works 15 hours at macdonalds (m=15) find the number of hours w:

You have the next system of inequalities:

`\begin{gathered} m+w\le20 \\ 12m+8w\ge200 \end{gathered}`

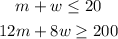
Substitute the m in both equations for 15 and find the minimum number of whole hours washing cars (w):

`\begin{gathered} 15+w\le20 \\ 15-15+w\le20-15 \\ w\le5 \\ \\ 12(15)+8w\ge200 \\ 180+8w\ge200 \\ 180-180+8w\ge200-180 \\ 8w\ge20 \\ w\ge(20)/(8) \\ w\ge2.5 \end{gathered}`

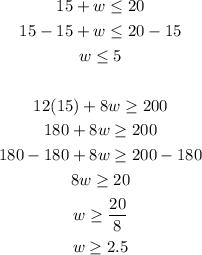
As you can see if he works 15 hours in mcdonalds, he needs to work a minimum of 3 whole hours (2.5 ≤ w ≤ 5) washing cars to meet his requirements (work at most 20 hours and earn minimum $200)

Answer: he needs to work a minimum of 3 whole hours washing cars