Question

The following probability distribution was obtained in a sandwich shop. The random variable x represents the number of condiments used for a hamburger Use the probability distribution table below to find the mean and standard deviation for therandom variable x

Answer 1

To figure out the mean, we will use the formula below

`\sum_{n\mathop{=}0}^4x.P(x)`

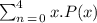
when x=0

`x.P(x)=0*1.30=0`

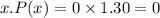
When x=1

`x.P(x)=1*0.40=0.40`

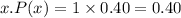
when x=2

`x.P(x)=2*0.20=0.40`

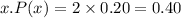
When x=3

`x.P(x)=3*0.06=0.18`

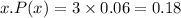
When x= 4

`x.P(x)=4*0.04=0.16`

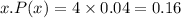
Hence,

The mean of the distribution will be

`\sum_{n\mathop{=}0}^4x.P(x)=0+0.40+0.40+0.18+0.16=1.14`

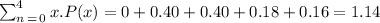
Hence,

The mean is

`\Rightarrow1.14`

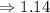
To figure out the standar deviation, we will use the formula below

`\sigma^2=\sum_{n\mathop{=}1}^4(x-\mu)^2P(x)`

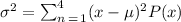
when x=0

`(0-1.14)^2*0.30=0.38988`

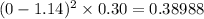
when x= 1

`(1-1.14)^2*0.40=0.00784`

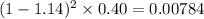
when x=2

`(2-1.14)^2*0.20=0.14792`

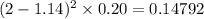
When x=3

`(3-1.14)^2*0.06=0.20758`

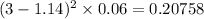
When x=4

`(4-1.14)^2*0.04=0.327184`

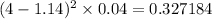
Add them up and find the square root

`\begin{gathered} \sigma^2=0.38988+0.00784+0.14792+0.20758+0.327184 \\ \sigma^2=1.080404 \\ \sigma=√(1.080404) \\ \sigma=1.04 \end{gathered}`

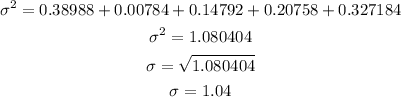
Hence,

The mean = 1.14 and the standard deviation is =1.04

OPTION A is the right answer