Question

A police car approaches an observer with its siren on at a constant velocity. The observer hears the siren with a frequency of 410 Hz as the car apporaches. After the car has past the frequency drops to 376 Hz. How fast was the police car traveling to the nearest tenth of a meter per second?

Answer 1

28.4 m/s.

Explanation:

Given:

Actual frequency of the sound waves (f) = 376 Hz

Observed frequency (f') = 410 Hz

Speed of sound (v) = 343 m/s

Speed of observer (vo) = 0 m/s

Speed of police car (vs) = ?

We have that the formula of the Doppler effect is the following:

`\begin{gathered} f^(\prime)=(v+v_o)/(v-v_s)\cdot f \\ \\ \text{ We replacing:} \\ \\ 410=(343+0)/(343-v_s)\cdot376 \\ \\ 410=(128968)/(343-v_s) \\ \\ 410\left(343-v_s\right)=128968 \\ \\ 343-v_s=(128968)/(410) \\ \\ v_s=343-(128968)/(410) \\ \\ v_s=28.4\text{ m/s} \end{gathered}`

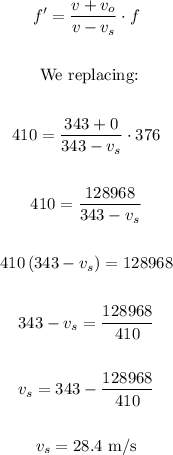
The speed of the police car is 28.4 m/s.