GIVEN:
We are given a circle with center P, a radius of length 8cm and an arc AB with length 7cm.
Required;
To find the angle measure of the central angle APB of the circle given.
Step-by-step solution;
To find the central angle of the circle given the above information, we begin by taking note of the formula for the length of an arc, and that is;
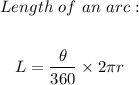
The variables given here are;
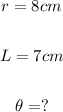
Now we will substitute the known values as follows;
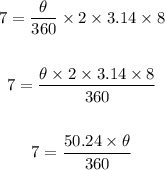
Next, we cross multiply;
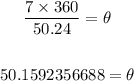
Rounded to the nearest degree, we now have;
ANSWER:
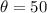
Option A is the correct answer.