Question

The height of a ball above the ground as a function of time is given by the functionℎ()=−32^2+8+3where h is the height of the ball in feet and t is the time in seconds. What is the maximum height of the ball? Round to the nearest tenth (one place past the decimal)

Answer 1

`3.5ft`

Step-by-step explanation

The height of the ball is given by the function:

`h(t)=-32t^2+8t+3`

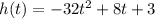
To find the maximum height of the function, we have to find the value of h(t) when t is:

`t=-(b)/(2a)`

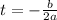
where b = coefficient of t = 8

a = coefficient of t² = -32

Therefore, we have:

`\begin{gathered} t=-(8)/(2(-32))=-(8)/(-64) \\ t=0.125 \end{gathered}`

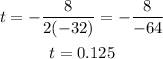
Now, find h(0.125):

`\begin{gathered} h(0.125)=-32(0.125)^2+8(0.125)+3 \\ h=-0.5+1+3 \\ h=3.5ft \end{gathered}`

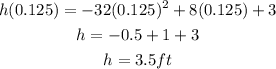
That is the maximum height of the ball.