Question

I am attaching a picture of the question as you can see the answer has already been picked well my teacher wants me to show how she got that answer.

Answer 1

From the properties of the circle we know that:

`\begin{gathered} 6(2x-2+6)=5(31+5) \\ 6(2x+4)=5(36) \\ 12x+24=180 \\ 12x=180-24 \\ 12x=156 \\ x=(156)/(12) \\ x=13 \end{gathered}`

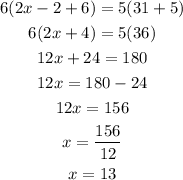
This comes from the fact that If two secants are drawn to a circle from one exterior point, then the product of the external segment and the total length of each secant are equal. In this case this means that:

`DE\cdot DF=DC\cdot DB`

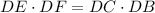
Now that we know the value of x we plug it in the expression for EF:

`2(13)-2=26-2=24`

Therefore segment EF is equal to 24.