From the statement of the problem we know that:
• we have a right triangle,
,
• the hypotenuse (H) is twice the length of one of its legs (a), so we write:
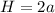
• the other leg (b) has a length:
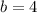
in feet.
From Pitagoras Theorem we know that:
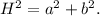
Replacing the equations for H and b, we have that:
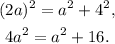
Solving the last equation for a, we get:
![\begin{gathered} 4a^2-a^2=16, \\ 3a^2=16, \\ a^2=(16)/(3), \\ a=\sqrt[]{(16)/(3)}, \\ a=\frac{4}{\sqrt[]{3}}\cong2.31. \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/v5rkd9qel8xa1nx62lxdxgq9zdxk44kpc0.png)
The hypotenuse of the triangle:

Answer
The legs of the triangle are 4 and 2.31 feet and the hypotenuse is 4.62 feet,