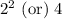The given statement is,
To solve
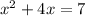
by completing the square add ______ ono both sides of the equation.
To fill the blank:
We know that the identity,
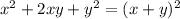
Comparing the equating terms as follows,
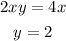
Then, add on both sides of the equation by,
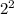
Hence, the answer is,