Question

`y = 2x + 2 \\ y = 7x + 11`how do you solve this equation with substitution?

Answer 1

`x=-(9)/(5),y=-(8)/(5)`

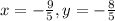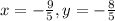
1) As the chosen method to solve this Linear System of equations then we can write out the following:

`\mleft\{\begin{matrix}y=2x+2 \\ y=7x+11\end{matrix}\mright.`

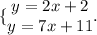
2)Let's start with the simplest equation between them. And then, plug into that the value of "y". This way:

`\begin{gathered} \mleft\{\begin{matrix}I)y=2x+2 \\ II)y=7x+11\end{matrix}\mright. \\ I)y=2x+2 \\ 7x+11=2x+2 \\ 7x+11-2x=2x-2x+2 \\ 5x+11=2 \\ 5x+11-11=2-11 \\ 5x=-9 \\ (5x)/(5)=-(9)/(5) \\ x=-(9)/(5) \end{gathered}`

Now, that we know the quantity of "x", let's plug it into any one of those equations.

3)Let's pick the 2nd one and solve it for "y".

`\begin{gathered} y=7x+11,x=-(9)/(5) \\ y=7(-(9)/(5))+11 \\ y=-(63)/(5)+11 \\ y=-(63)/(5)+(55)/(5) \\ y=-(8)/(5) \end{gathered}`

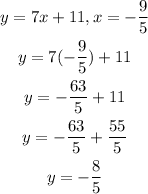
Thus, the answer is:

`x=-(9)/(5),y=-(8)/(5)`