We are asked to describe sequence of transformations used to produce the graph for each function.
First of all, let us understand transformation rules for functions.
Vertical Translation:
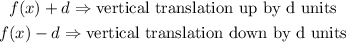
Horizontal Translation:
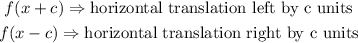
Reflection:

Dilation:
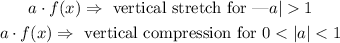
Function 14:
![y=-\sqrt[]{x+4}+1](https://img.qammunity.org/2023/formulas/mathematics/college/brb0t5o6u2az1r6l7fc39t0fuq89n4v701.png)
As you can see,
it is reflected over the x-axis
(x+4) means translated left by 4 units
Also, +1 translated up by 1 unit
Function 15:
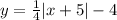
As you can see,
It is vertically compressed by 1/4
(x+5) means translated left by 5 units
Also, -4 means translated down by 4 units
Function 16:
![y=\sqrt[3]{-x}+5](https://img.qammunity.org/2023/formulas/mathematics/college/y6n2fjntizpmt166y1uqs0xa8frfpfoe7q.png)
As you can see,
it is reflected over the y-axis since f(-x)
+5 means translated up by 5 unit
Function 17:
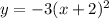
As you can see,
it is reflected over the x-axis
(x+2) means translated left by 2 units
Also, It is vertically stretched by 3
Function 18:
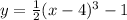
As you can see,
(x - 4) means translated right by 2 units
-1 means translated down by 1 unit
Also, It is vertically compressed by 1/2