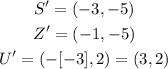A rotation is a transformation in a plane that turns every point of a preimage through a specified angle and direction about a fixed point.
Rotating a figure 270 degrees clockwise is the same as rotating a figure 90 degrees counterclockwise. The rule is:
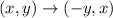
The coordinates of the vertices of the triangle are given to be:
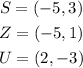
Applying the rule, we have the transformed points to be: