Given a figure of a cone
as shown, the radius of the base = r = 10 in
And the height = h = 24 in
The lateral area (LA) will be given using the formula:
![\begin{gathered} LA=\pi\cdot r\cdot l \\ l=\sqrt[]{r^2+h^2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3olq28i2dp3oit3cu0west0xzexvnm5wbg.png)
So, first, we'll find the value of (l) from r, and h
![l=\sqrt[]{10^2+24^2}=\sqrt[]{100+576}=\sqrt[]{676}=26\text{ in}](https://img.qammunity.org/2023/formulas/mathematics/college/pr2ld4m4dp39nb2alxhh35tf0kb942we7m.png)
Then, substitute with (r) and (l) to find (LA):
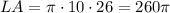
So, the answer will be LA = 260π in²