ANSWER:
16 songs
Step-by-step explanation:
Given:
Cost of each download = $0.75
Kevin has $25.
After downloading he has a balance of $13.
The equation will be:
0.75x + 13 = 25
where x represents number of MP3 downloaded
To find how many songs he can download, let's solve for x;
0.75x + 13 = 25
Subtract 13 from both sides of the equation:
0.75x + 13 - 13 = 25 -13
0.75x = 12
Divide both sides by 0.75:
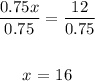
Kevin can download 16 songs.
Let's graph the solution on a number line below