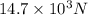Question

A 12 gram bullet is accelerated from rest to 7.0X102 m/s as it travels down a 20. cm yun barrel. Pasume constant acceleration. What was the accelerating force

Answer 1

Remember the following formula that relates the initial and final velocites of an object moving along a distance d at a constant acceleration a:

`v^2_f=v^2_0+2ad`

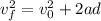
Since the bullet starts at rest, then the intial velocity is 0:

`\Rightarrow v^2_f=2ad`

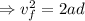
Isolate a from the equation:

`\Rightarrow a=\frac{v^2_f_{}}{2d}`

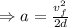
Substitute v_f=70x10^2 m/s and d=20cm:

The net force is equal to the mass of the object times its acceleration, according to the Newton's Second Law of Motion:

`F=ma`

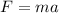
Substitute the value of the acceleration that was found previously, and m=12g:

`\begin{gathered} F=(12g)(1.225*10^6(m)/(s^2)) \\ =(12*10^(-3)kg)(1.225*10^6(m)/(s^2)) \\ =14,700N \end{gathered}`

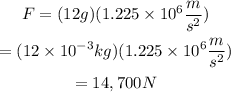
Therefore, the value of the acceleration force, was:

`14.7*10^3N`