Question

Find the equation of the parabola with its focus at (6,2) and its directrix y = 0.

Answer 1

As per given by the question,

There are given that focus point at (6, 2) and line y=0.

Now,

Distance from line dL=distance from the point dF

Then,

`y=\sqrt[]{(x-x_1)^2+(y-y_1)^2^{}_{}}^{}`

Now,

`\begin{gathered} y=\sqrt[]{(x-x_1)^2+(y-y_1)^2^{}_{}}^{} \\ y=\sqrt[]{(x-6)^2+(y-2)^2} \end{gathered}`

Then,

Square on the both side of the equation,

`\begin{gathered} y^{}=\sqrt[]{(x-6)^2+(y-2)^2} \\ y^2=(x-6)^2+(y-2)^2 \end{gathered}`

According to the question,

There are given that y=0,

So,

`\begin{gathered} y^2=(x-6)^2+(y-2)^2 \\ y^2=x^2+36-12x+y^2+4-4y \\ y^2=x^2+y^2-12x-4y+40 \end{gathered}`

Now,

`\begin{gathered} x^2-12x-4y+40=0 \\ x^2-12x+40=4y \end{gathered}`

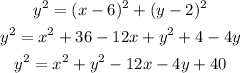
Now, find the value of jy from above equation;

`\begin{gathered} 4y=x^2-12x+40 \\ y=(1)/(4)(x^2-12x+40) \end{gathered}`

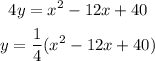
So,

`\begin{gathered} y=(1)/(4)((x-6)^2+4) \\ y=(1)/(4)(x-6)^2+1 \end{gathered}`

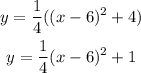
Hence, the option D is correct.