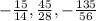Question

Find the next three terms in the geometric sequence. 20/63 -10/21 5/7

Answer 1

By definition, a Geometric sequence is that sequence in which a term is found by multiplying the previous one by the "Common ratio". The Common ratio is constant.

In this case you have the folowing Geometric sequence:

`(20)/(63),-(10)/(21),(5)/(7),\ldots`

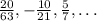
In order to find the Common ratio of this sequence, you can divide one of the given term by the previous term, as you can see below:

`r=-(10)/(21)/(20)/(63)=((-10)(63))/((21)(20))=-(3)/(2)`

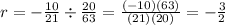
Therefore, you can set up the following equation for this sequence:

`a_n=((20)/(63))(-(3)/(2))^((n-1))`

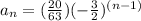
Because the formula for a Geometric sequence is:

`a_n=a_1(r)^((n-1))_{}`

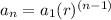
Where:

- The nth term is

`a_n`

- The first term is

`a_1`

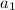
- The common ratio is "r".

- The term position is "n".

Since, in this case

`\begin{gathered} r=-(3)/(2) \\ \\ a_1=(20)/(63) \end{gathered}`

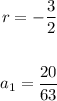
You can find the next three terms in the given sequence as following:

`\begin{gathered} a_4=((20)/(63))(-(3)/(2))^((4-1))=-(15)/(14) \\ \\ a_5=((20)/(63))(-(3)/(2))^((5-1))=(45)/(28) \\ \\ a_6=((20)/(63))(-(3)/(2))^((6-1))=-(135)/(56) \end{gathered}`

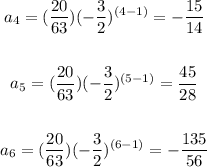
Therefore, the answer is:

`-(15)/(14),(45)/(28),-(135)/(56)`