Answer:
703 yds
Step-by-step explanation:
To find the distance (i.e. the values of a), apply trigonometrical ratio.
• The side ,opposite ,angle 50 degrees, BC = a
,
• The side ,adjacent to ,angle 50 degrees, AC = 590 yds
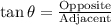
Therefore:
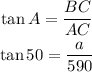
Cross multiply:
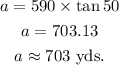
The distance across the lake is 703 yards (to the nearest whole number).