Question

At the top of a 100 m tall building, a 3 kg ball is dropped from rest. The ball strikes the ground with a speed of 30 m/s. How much energy is lost to air friction?Use g = 10 m/s2

Answer 1

Given,

The height of the building, h=100 m

The mass of the ball, m=3 kg

The speed of the ball when it strikes the ground, v=30 m/s

The acceleration due to gravity, g=10 m/s

The energy lost in the air friction is equal to the difference in the energy of the ball when it was at the top of the building at rest and the energy when it strikes the ground.

When the ball was at the top of the building it had only potential energy. As it was dropping it slowly lost potential energy and gained kinetic energy. When it hits the ground it only has kinetic energy and no potential energy.

Thus the difference in the energy of the ball when it was at the top and that when it hits the ground is given by,

`\begin{gathered} \Delta E=mgh-(1)/(2)mv^2 \\ =m(gh-(v^2)/(2)) \end{gathered}`

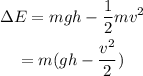
On substituting the known values,

`\begin{gathered} \Delta E=3(10*100-(30^2)/(2)) \\ =1650\text{ J} \end{gathered}`

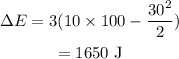
Thus the energy lost by the ball due to air friction is 1650 J