The equation in the question is given below
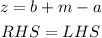
To solve for a, we will, first of all, identify the coefficient of a
The coefficient of a is

To make a positive we will take a to the R.H.S and then take z to the L.H.S
Hence, we will have
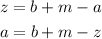
Hence,
The equation for a will be
a= b + m - z