Given:
z1 = 6(cos80 + isin80)
z2 = 8(cos140 + isin140)
Let's solve for the following:
(a) z1/z2
To solve for z1/z2, we have:
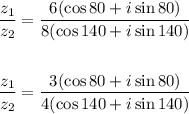
Solving further:
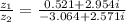
Multiply the denominator and numerator by the conjugate:
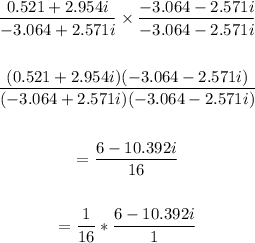
Let's write in trigonometric form:
![\begin{gathered} 0.0625(6-10.392i) \\ \\ 0.0625(6)+0.0625(-10.392i) \\ \\ 0.375-0.649i \\ \\ \lvert z\rvert=\sqrt[]{(-0.649)^2+(}0.375)^2 \\ \\ \lvert z\rvert=\sqrt[]{0.562}=0.749 \\ \\ \tan ^(-1)((-0.649)/(0.375))=-60^o \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hflkj6agw87jii3fspnxv8u881mr2fwvqo.png)
Therefore, the answer in trigonometric form is:
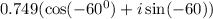
Part b.
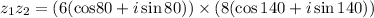
Thus, we have:
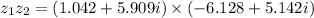
Apply the FOIL method:
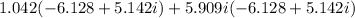
Apply distributive property:
![undefined]()