Question

pure acid is to be added to a 20% acid solution to obtain 52L of a 40% acid solution.What amounts of each should be used?

Answer 1

Let's define the following variables:

x = the amount of pure acid (100%) in liters

y = the amount of 20% acid in liters

If mixing the two liquids makes 52 L, then we can say that: (equation1)

`x+y=52`

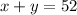
In addition, 100% of x liters + 20% of y liters will make 52L of 40% solution then, we can also say that: (equation 2)

`\begin{gathered} 1(x)+0.2(y)=0.4(52) \\ x+0.2y=20.8 \end{gathered}`

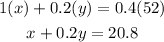
Using this two equations, we can solve for the values of x and y using elimination. Here the steps:

1. Subtract equation 2 from equation 1.

`\begin{gathered} x+y=52 \\ x+0.2y=20.8 \\ \text{Subtract similar terms in the two equations above.} \\ 0.8y=31.2 \end{gathered}`

2. Divide both sides of the equation by 0.8.

`\begin{gathered} (0.8y)/(0.8)=(31.2)/(0.8) \\ y=39 \end{gathered}`

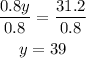
Therefore, the value of y = 39. The amount of 20% acid solution added to the mixture is 39 liters.

3. Plug in the value of y in the equation 1 to solve for x.

`\begin{gathered} x+y=52 \\ x+39=52 \\ x=52-39 \\ x=13 \end{gathered}`

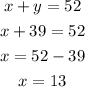
The value of x is 13. Hence, the amount of pure acid that was added to the mixture is 13 liters.