Question

What is the measure of m?n20m5m = [?]V=Give your answer in simplest form.

Answer 1

Take into account that you have two right triangles inside the bigger triangle. Then, by using the Pythagorean theorem in the smaller triangle, you have:

`m^2=5^2+n^2`

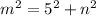
for one of the legs of the bigger triangle you obtain:

`c^2=(20+5)^2-m^2`

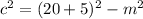
where c is a leg of the bigger triangle. For the second interior triangle:

`c^2=n^2+20^2`

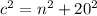
Now, replace the expression for c^2 of the second equation, in the third equation and solve for n^2:

`\begin{gathered} (20+5)^2-m^2=n^2+20^2 \\ n^2=(20+5)^2-20^2-m^2 \end{gathered}`

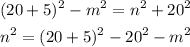
Then, solve for n^2 in the first equation, replace the obtained result into the pervious equation and solve for m, as follow:

`\begin{gathered} n^2=m^2-5^2^{} \\ m^2-5^2=(20+5)^2-20^2-m^2 \\ m^2+m^2=(20+5)^2-20^2+5^2 \\ 2m^2=25^2-20^2+5^2 \\ 2m^2=625-400+25 \\ m^2=(250)/(2) \\ m=\sqrt[]{125}=\sqrt[]{5\cdot25}=5\sqrt[]{5} \end{gathered}`

Hence, the value of m is m = 5√5