Question

What is the distance from point A to point C?A.4 unitsB.5 unitsC.8 unitsD.9 units

Answer 1

C. 8 units

Step-by-step explanation

there are 2 ways to solve this,

Step 1

using the distance between 2 points formula

is says

for 2 points

`\begin{gathered} P1(x_1,y_1) \\ P2(x_2,y_2) \end{gathered}`

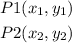
the distance between P1 and P2 is given by the expression

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

so

let

P1=A=(-4,4)

P2=C=(4,4)

now, replace in the expression

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d_(AC)=\sqrt[]{(4-(-4))^2+(4-4)^2} \\ d_(AC)=\sqrt[]{(4+4)^2+(0)^2} \\ d_(AC)=\sqrt[]{(8)^2} \\ d_(AC)=8 \end{gathered}`

so, the distance from point A to point C is 8 units

Step 2

the second method is by checking the graph : this is only valid for 2 points that make a horizontal line ,this measns both coordinates have the same y-value

`\begin{gathered} A=(-4.4) \\ C=(4,4) \end{gathered}`

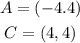
so, count the squares in the graph

therefore, the answer is

C. 8 units

I hope this helps you