For the transaction given, we shall apply a simple interest formula which is;

Note however that the time in this instance is not up to 1 year but a fraction of 1 year, that is;
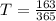
Therefore, the interest shall be calculated as follows;
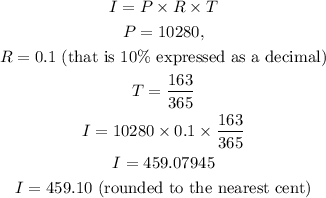
The amount to be repaid after 163 days would be the principal plus the interest and that would be;
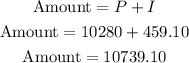
ANSWER:
Amount to be repaid is $10,739.10