Answer:
Step-by-step explanation:
First, we solve the value/s of x to make a graph for the equation:
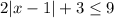
So,we add -3 to both sides:
2|x-1|+3-3≤9-3
Simplify
2|x-1|≤6
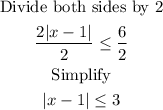
Then, we apply the absolute rule: If |u|≤a, a>0 then -a≤u≤a.
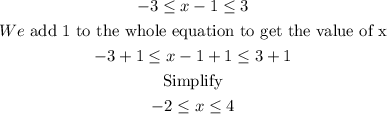
The values are:
x≤ 4 and x ≥ -2
Therefore, the graph is: