Question

brad owns a news stand that has room for 100 newspaper per day. in his town there are 2 papers, the journal and the globe. everyday, Brad sells 20 journals and 25 globes to costumers with subscriptions. If Brad makes $0.05 for every journal sold and $0.10 for each globe sold, how many journals and how many globes should he put on his stand to make the most money ? it must include the problem, the constraints, the graph of the feasible region properly shaded and the vertices labeled (it can be done on desmos ), the objective function, a table of values analyzing the vertices( finding the max and min values ) and a paragraph explaining your findings

Answer 1

let

a = journal

b = globes

Since the stand can only contain 100 newspapers,

`a+b\leq100`

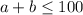
The constraint will be

`\begin{gathered} a+b\leq100 \\ a\ge20 \\ b\ge25 \end{gathered}`

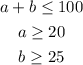
To maximize profits

`\text{p}=0.05a+0.10b`

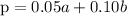
let us represent it with a graph. The corner point (vertices) will be

(20, 25)

(20, 80)

(75, 25)

Therefore,

The maximum profit will be

`\begin{gathered} \text{p}=0.05a+0.10b \\ \text{p}=0.05(20)+0.10(80)=1+8=\text{ \$9} \end{gathered}`

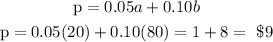
He should sell 20 journals and 80 globes to get the maximum profit($9)