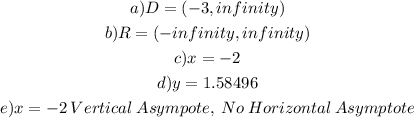
a) Let's find the Domain of that logarithmic function by finding the values that are undefined for this function, so we can do the following:
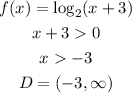
Note that the argument of a logarithm must be greater than 0.
b) Range
For the range, we can find the Range of this function by doing this:
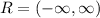
Since there are no discontinuities along with the function.
c) The x-intercept
We can plug into that y=0 and find the x-intercept
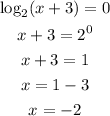
d) What is the y-intercept
Similarly, we can plug into the function x=0
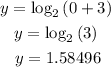
e) Asymptote
The asymptote is the line that demarks the points that the graph won't trespass:
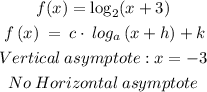
Note that the vertical asymptote is located at the value of h