Question

700 randomly selected Americans were asked if they believed the minimum wage should beraised. 350 said yes. Construct a 90% confidence interval for the proportion of Americanswho believe that the minimum wage should be raised.A. (0.469, 0.531)B.(0.481, 0.519)C.(0.431, 0.569)D.(0.347, 0.630)

Answer 1

`A)0.469,0.531`

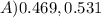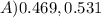
1) The first thing to consider when we tackle this question, is to make use of a z-score to construct that required interval of confidence: 90%

2) Let's gather from the data and write out the following:

`\begin{gathered} n=700,\pi=(350)/(700),\alpha=0.9 \\ p=(1+\alpha)/(2)=(1+0.9)/(2)=.95 \\ z=1.645 \\ \end{gathered}`

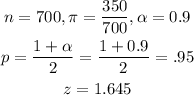
Note that we resorted to a table to find the z score.

2.2. The next step is to figure out the Lower and the Upper Limits :

`\begin{gathered} Lower\: Limit\colon \\ \pi-z\sqrt[]{(\pi(1-\pi))/(n)}=(350)/(700)-1.645\sqrt[]{(0.5(1-0.5))/(700)}=.4689 \\ Upper\: Limit\colon \\ \pi+z\sqrt[]{(\pi(1-\pi))/(n)}=(350)/(700)+1.645\sqrt[]{(0.5(1-0.5))/(700)}=.5311 \end{gathered}`

Once we have the lower and the upper limit, we can state that the answer is:

`A)0.469,0.531`