Step 1
Use a calculator to find the first term that equals 0 to the nearest hundredth-thousand
The first term that equals zero to the nearest hundred thousandth is; n= 21

Step 2
The pendulum will not stop mathematically because the nth term is given as;
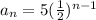
Can approach zero but will never be zero
Step 3
At 10 swings the total distance traveled will be;
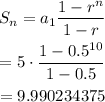
At 50 swings the total distance traveled will be;
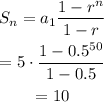
Step 4
My observation and conclusion are that the Pendulum swings at distances that follow a geometric progression and the total distance traveled will be about 10.