Question

Is there anyone who can help with this problem? Thanks

Answer 1

D. 2 imaginary, 2 real

EXPLANATION :

From the problem, we have :

`f(x)=x^4+12x^3+37x^2+12x+36`

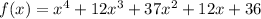
Using synthetic division :

Let's test x = -6 which is a factor of 36

The coefficients are 1, 12, 37, 12 and 36

The operations performed are addition (bring down 1) then multiply it by the divisor :

1(-6) = -6 and write it below the next term and so on and so forth.

Since the last result is 0, we can say that -6 is a factor of the polynomial.

The polynomial now will be :

`f(x)=(x+6)(x^3+6x^2+x+6)`

Factor the second parenthesis by grouping :

`\begin{gathered} x^3+6x^2+x+6=(x^3+6x^2)+(x+6) \\ =x^2(x+6)+(x+6) \\ =(x^2+1)(x+6) \end{gathered}`

The polynomial now will be :

`f(x)=(x+6)(x+6)(x^2+1)`

To check the roots, equate the factors to 0.

`\begin{gathered} x+6=0 \\ x=-6 \\ \\ x+6=0 \\ x=-6 \\ \\ x^2+1=0 \\ x^2=-1 \\ x=\pm√(-1) \\ x=\pm i \end{gathered}`

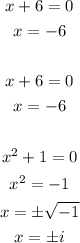
So there are 2 real and 2 imaginary roots