Question

Sorry I cut off the end, which is “ what will the value of the car be after 4 years? Round your answer to the nearest hundredth?”

Answer 1

You know that the price of the car when Mariah purchased it was:

`$8,599$\text{ }dollars`

And you also know that the rate of depreciation is 2.5%.

Then, you can use the following formula to calculate the Depreciation Value:

`A_n=P(1-R)^n`

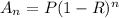
Where "P" is the initial value, "R" is the depreciation rate (as a Decimal number), and "n" is the number of periods.

You can identify that, in this case:

`\begin{gathered} P=$8,599$ \\ \\ R=(2.5)/(100)=0.025 \\ \\ n=4 \end{gathered}`

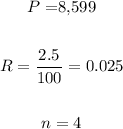
Then, substituting values into the formula and evaluating, you get this result (in dollars):

`\begin{gathered} A_n=P(1-R)^n=($8,599$)(1-0.025)^4\approx7,770.81 \\ \end{gathered}`

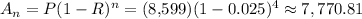
Therefore, the answer is: Last option.