Question

Consider the function: f(x) = x^3 - x^2 - 6x Determine the instantaneous rate of change at:a) x= -1b) x= 4

Answer 1

The instantaneous rate of change is the derivative of the function so lets calculate it:

`\begin{gathered} f^(\prime)(x)=(df)/(dx)=(d)/(dx)(x^3-x^2-6x) \\ =3x^2-2x-6 \end{gathered}`

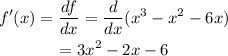
Now that we know the derivative to find the instantaneous rate at a given value we just evaluate it at that point.

a)

If x=-1, then:

`\begin{gathered} f^(\prime)(-1)=3(-1)^2-2(-1)-6 \\ =3(1)+2-6 \\ =3+2-6 \\ =5-6 \\ =-1 \end{gathered}`

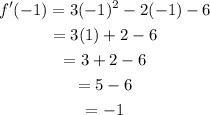
Therefore the instantaneous rate of change at x=-1 is -1.

b)

If x=4, then:

`\begin{gathered} f^(\prime)(4)=3(4)^2-2(4)-6 \\ =3(16)-8-6 \\ =48-8-6 \\ =34 \end{gathered}`

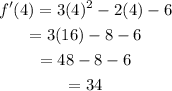
Therefore the instantaneous rate of change at x=4 is 34.