Question

Find the open interval where the function is increasing and decreasing.y=x^2+2x+3

Answer 1

Step-by-step explanation:

Step 1. The equation we have is:

`y=x^2+2x+3`

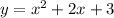
This is a quadratic equation which will be represented by a parabola.

Step 2. We need to find the open interval where the function is increasing and decreasing. For a parabola with a vertex at (h,k), the decreasing and increasing parts are shown in the following diagram:

Note: the diagram is a general illustration, not the parabola for the given function.

As you can see the function is decreasing until the vertex, and from the vertex to the right, it starts to increase.

Step 3. We can conclude that in general, the function decreases in the interval

`(-\infty,h)`

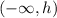
And increases from h to infinity:

`(h,\infty)`

Where h is the x-value of the vertex.

Step 4. To find the value of h, we need to find the vertex of the parabola.

Remember that the equation given is:

`y=x^(2)+2x+3`

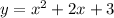
We need to write this equation in the vertex form: