Solution:
Given:

To solve using the substitution method, we make one unknown in one of the equations the subject of the formula and substitute it into the other equation.
From the given equations, make y the subject of the formula in equation (2);
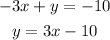
Substituting y into equation (1);
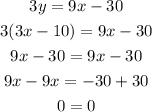
The solution shows the system has an infinite number of solutions.