Question

6. Use Limit Comparison Test to determine whether the series is convergent or divergent:

Answer 1

Given the following series:

`\sum(3+2n)/((2+n^2)^2)`

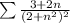
We will use the limit Comparison Test to determine whether the series is convergent or divergent.

The limit will be as follows:

`\begin{gathered} lim_(n\rightarrow\infty)(a_n)/(b_n) \\ a_n=(3+2n)/((2+n^(2))^(2)) \\ b_n=(2n)/(n^4)=(2)/(n^3) \end{gathered}`

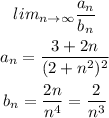
So, Substitute with (a) and (b) into the limit then calculate the limit:

Divide both the numerator and the denominator by n⁴ then substitute

n = ∞, so, the result will be:

`=(2)/(2)=1`

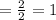
As the value of the limit is finite and positive

So, both the series are convergent or divergent

The series (b) is convergent

So, the given series is convergent